2017年!めでたい年になりますように!
2017年ですよ!
年が明けてからしばらく経ちましたが、新年一発目のブログをスズキが書きます。
めでたい話を...
冬はスキー以外は家に引きこもる私が、友人に引きずられてゲームセンターに行ってました。
そこでテレビの録画をひたすら流しているUFOキャッチャーが!
テレビ番組は「月曜から夜更かし」キャッチャーの景品はなんと… 宝石!!
早速挑戦、ポロポロとれました笑

宝石はきっとめでたい!今年1発目はそんなお話をしたいと思います。
ダイヤモンド
近年はカーボンファイバー素材などで工業でも大活躍!原子番号6番「炭素」さんです。
鉛筆の芯や炭と同じ原料というのは皆さんもよくご存知かと思います。
今回は同じ炭素原子で構成されている黒鉛とダイヤモンドがなぜそこまで違いがあるのか?について簡単に紹介できたらと思います。
炭素分子の結合の違い
ダイヤモンドと黒鉛では炭素分子の結合が異なります。
炭素には電子対と呼ばれる手が4本あります。
それぞれ炭素分子は主に「共有結合」「ファンデルワールス力」で原子同士お互い手を結んでいます。
ダイヤモンド
原子間は電子対の共有結合をされていて、分子構成も美しいぐらい均等に配列されています。
分子構造は立体的な幾何構造です。
天然で幾何構造が生まれるのは神秘的です。
おわりに
今回獲得した宝石がホンモノなのかは分かりません。鑑定してもらうのも怖いです。笑
宝石学と呼ばれる学問もあるそうで、ちょっと興味をそそられました。
身近なものに疑問をもって調べると新たな見え方、発見をできるのはとても面白いです。
次回もそんな身近なモノをプチ化学を交えながらご紹介できたらなと思います。
以上、皆様も今年は良い年になりますよう!さようなら!
リラックス方法
今回のブログ担当のカキノです。
現代社会はストレスに満ち溢れているといわれていますが、
貯め込んでいてもプラスには働きません。
今回は私のリラックス方法について少し紹介します。

私のリラックス方法は珈琲を淹れることです。
缶コーヒーもおいしいですが、挽きたての豆から淹れると最高においしいです。
様々な抽出機器がありますが、
ドリッパー、フレンチプレス、直火式エスプレッソ
を使用しています。
それぞれに特徴があり、楽しめる珈琲も変わってきます。
同じコーヒー豆を使用しても、焙煎度合や挽き方、湯温、淹れ方により、
味や香りも変わってきます。
好みの味を見つけるのも一つの楽しみです。
毎回同じ味で淹れられるよう調整するのも楽しみです。
・リラックス効果
・脳の活性化
・うつ病の防止
・糖尿病予防
珈琲にはこのような効果があるそうで、
珈琲の香りを嗅ぐことで脳波が多く出ておりリラックス効果があるそうです。
ブログでは香りはお届けできませんが、
皆さんも何か楽しいリラックス方法を探してみてはいかがでしょうか?
モチベーション
最近、ますます親バカ発揮中の寺田です。土日の家族サービス万歳!
そんな私からは今回「モチベーション」について書きたいと思います。
日々安定したパフォーマンスを発揮するには、それなりの「モチベーション」が必要です。
満足いく報酬、働きやすい職場、自分の興味のある内容など、これは人それぞれだと思います。
全てに満足いく職場や業務はそう簡単には存在しません。
そしてこれらに何らかの不満が生じた場合、モチベーションは著しく低下します。
ではモチベーションを上げるまたは保つにはどうしたら良いのでしょうか?
その方法について考察してみたいと思います。
プラスへの変換
日々の業務で不満が発生しない事はないに等しいと考えます。
(不満がない人もいるでしょうが、少数派でしょう)
そもそもそれを不満と思うかどうかは人によると思います。
自分にとってマイナスと考えた瞬間、「不満」に変わるわけですが、
それならばマイナスではなくプラスに考えれば良いのではないでしょうか?
例えば、理不尽な内容の仕事を割り振られたとします。
誰しも最初は「やだなぁ」「無理でしょ」と思う事でしょう。
そしてこの仕事は恐らく、他の人はやりたくない事なのでしょう。
「なんで自分が?」「他の人がやればいいのに」とマイナスの感情が沸き
モチベーションが大きく低下してしまう事が想像できます。
しかし、これをプラスへ転換させる事も可能です。
もちろんこれはこのマイナスをプラスへ転換するパワーが必要ですが、
プラスに出来た時、最高の達成感と自信を得る事にも繋がります。
この場合、誰もやりたくない→誰もやったことがない→自分だけがノウハウを得るという変換をしてみます。
最初は当然苦労しますが、徐々に知見を得る内に要領が掴めてきます。
すると、そこに関わる内容で問題が起こった際のキーマンになる事ができます。
キーマンになるという事は少なからず信頼されているという事を実感できます。
これによりモチベーションを上げる事が期待できます。
簡単に達成可能な目標設定
仕事する上で目標設定をしている人は多いと思います。
しかし、その目標がハードルを上げすぎて達成できずに終わり、結果モチベーションが下がっている人
もいるのではないでしょうか?あ設定によって、「達成」の確率を上げ、それを達成できる日を増やす事で
自分の自信に変えていく事が可能です。
日々成長を感じる事、少しでも前に進んでいる事を感じる事はモチベーションを上げる事に繋がり、
これを毎日続ける事ができるようになればこれがモチベーションの維持になります。
上記は自分自身でコントロールする方法ですので
外的要因
報酬、環境さえ良ければ良いという考えの方は、仕事内容ななんでも良く、
大変な仕事も苦にならない人もいるでしょう。
その代わり報酬が減る=モチベーション低下、環境が悪くなる=モチベーション低下となるため、
自分の考え方だけではどうにもなりません。
その場合は行動を起こす以外にないと思います。
報酬を上げるには、自分の働きが今の報酬に見合わないという事を周りに伝えるような行動を取る事になるでしょう。
環境を良くするには、自分が周りに働きかけ、自分の居場所を作る事になるでしょう。
いずれにしても自分から動かなければ何も変わりません。あれがやだ、これがやだと言ってるだけでは
何も変わらないのです。
ただ先を考えないで行動するのはおすすめしません。
先の見通しがたった時、一気に行動して状況を変えていく事が必要です。
現に私もiPXへの入社を決めた際、そうしています。
モチベーションは仕事だけとは限らず、日常生活におけるモチベーションもあります。
自分から行動して、環境を変えるには転職という選択肢もあります。
これによりモチベーションが上がる場合がありますが、その後モチベーションを維持するには
報酬・環境以外の仕事内容におけるポイントを作る事が大事であると考えます。
まとめ
人によって重きを置くところは違います。
自分にあった自分自身のコントロール方法を探す事が大事です。
モチベーションの維持は一生の課題であり、これを持続できてこそ
プロとしての仕事ができるのではないかと私は考えます。
自分の日々の生活を振り返り、マイナスな思考で働いている方は一度
モチベーションについて考えてみてはいかがでしょうか?
自分自身の考え方でなんとかなるならば、思考を変えてみてください。
明日からの職場での意識が変わるかもしれません。
日刊工業新聞社の主催でMBDセミナーを開催しました

EPLU(Engineering Process Leading Unit)の加藤です。
12月12日(月)に、日刊工業新聞社の主催でモデルベース開発(MBD)に関するセミナーを開催しました。
当日は、12名の方々に参加して頂きました。関東だけでなく、遠方から参加された方の方が多かったようです。
セミナーでは約3時間という時間の中で、MBDの概要から導入の考え方について、私の経験を交えながら紹介しました。
今回は日刊工業新聞社としても初めてのMBDセミナーということもあり、どのような方々が参加されるのか、受講者のレベルも全く想定できない状態だったため、こちらで準備した内容は少々詰め込みすぎだったかもしれません。
それでも、受講者の皆さまから積極的に質問も頂き、こちらも大変勉強になるセミナーとなりました。
またこのような機会があれば、さらに分かりやすいコンテンツを用意できたらと考えています。
参加頂いた受講者の皆さま、ありがとうございました。
「テスト」についての学習
今週のブログ担当の鈴木です。
業務で「テスト」を行うことがたびたびあるのため、その手法等について学習したいと思っております。
「テスト」は要求仕様通りの振る舞いをしているかの確認のために行われるものです。
その「テスト」の精度を上げることで、抜け漏れや見落としが減ることでより、品質は上がるでしょう。
何から手を付けるか
私が特に身につけたい点は2つございます。
①. テストケースの作成
②. 報告書の作成方法
上記2つを上げた理由としましては、大きくは抜け漏れの阻止のためです。
①のテストケース検討の時点で抜け漏れがあれば、それがそのまま不十分なテストになってしまうのは当然です。
②の報告書の作成も意図としては同じです。優れたテストを行っても、それを説明できるドキュメントがなければ絵に描いた餅と変わりません。また、理解しやすい資料を作ることは、テストケースの抜け漏れ防止にもつながると思います。
今後
今私の業務の現場では基本的には、指示されたテストを・指示された道具で行っておりますが
テストに用いるツール・環境についてもお客様にご提案できるように精進したいと思っております。
学習に用いているサイト
下記のサイト等を拝読いたしました。
この他にもテストや試験の手法ついては多くの書籍やwebサイトがあるため今後も継続して学習を続けていきたいと思っております。
ガウスの消去法をCで作ろう
今週のブログ担当のシロハと申します。
今回はいたって普通に"C言語”で”ガウスの消去法”のプログラムを作ろうと思います。
ガウスの消去法というと何?と思う方もいるかもしれませんが、
中身は「中学や高校で習う連立方程式を解くこと」と同じです。
ガウスの消去法よりも掃き出し法といったほうがなじみがあるかもしれませんね。
実際に計算してみる
ではプログラムを作る前に、簡単にガウスの消去法の計算プロセスについてのお話をします。
ガウスの消去法は2つのプロセスに分かれており、
1:前進消去
2:後退代入
と呼ばれる計算プロセスとなります。
ただし、先ほども述べたよう中・高で習う程度の計算であり内容はそんなに難しくありません。
ではプログラムを作る前に、まずは以下の例題を実際に計算してみます。
例:3x+6y+2z=32
x+2y+8z=40
7x+3y+3z=35
また後でコード化することも考えて、計算手順も示します。
今回の説明では、それぞれの要素を以下のように記述します

ではまず前進消去から始めます。
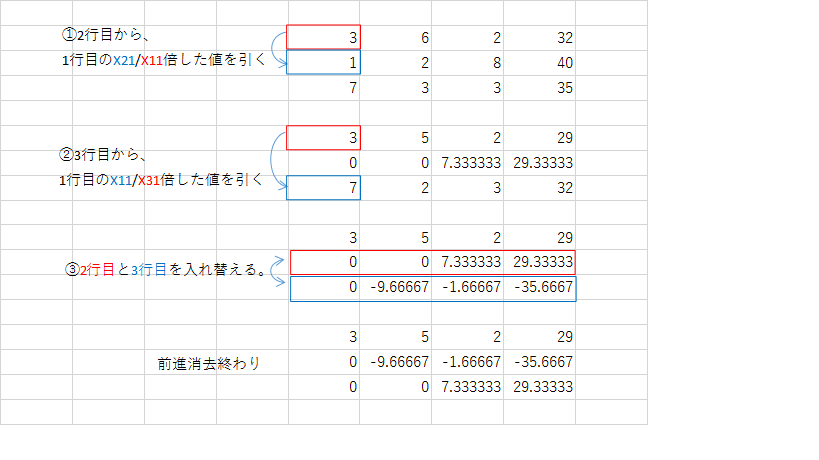
以上が前進消去の計算です。
このように、前進消去では左下部分を全て0にします。
また、前進消去では行の入れ替えが必要な場合もあります。
では次は後退代入です。

これで連立方程式の解を求めることが出来ました。
Cコードを書いてみる
計算の手順は分かったのでCコードを書いてみます。
#include <stdio.h> #include <math.h> #define N 4 void main(void) { int i=1,j=1,k=1,l=0,m=0; int end=0; //解がない時のフラグとして使用 double X[N][N],Y[N][N];//配列(Xは係数、Yは前進消去計算で行を入れ替えるときに使う) double sabun=0; //式の入力 X[0][0]=3;X[0][1]=6;X[0][2]=2;X[0][3]=32; X[1][0]=1;X[1][1]=2;X[1][2]=8;X[1][3]=40; X[2][0]=7;X[2][1]=3;X[2][2]=3;X[2][3]=35; for(i=0;i<N-1;i++) { for(j=0;j<N;j++) Y[i][j]=0; //配列Yの初期化 } //ここまで式入力 //前進消去 for(i=0;i<N-2;i++) { if(X[i][i]==0) //対角要素が0(前進消去③の入れ替えを行う判定) { for(l=i+1;l<N;l++) //入れ替え先を探す { if(X[l][l]!=0) //0ではない場所を見つけた { for(m=0;m<N;m++) //行の入れ替え { Y[i][m]=X[i][m];//入れ替え元を保存 X[i][m]=X[l][m]; X[l][m]=Y[i][m]; } break; } else if(l==N-1) { printf_s("解が一意に決まらない"); end=1; break; } } }//行の入れ替えはここまで for(j=i+1;j<N-1;j++) { sabun=X[j][i]/X[i][i]; //前進消去①、② for(k=i;k<N;k++) { X[j][k]-=sabun*X[i][k];//前進消去①、② } } if(end==1)break; //解が決まらないため計算終了 } //前進消去ここまで //後退代入 for(i=N-2;i>0;i--) { if(end==1)break; //解が決まらないため計算しない for(j=i-1;j>=0;j--) { sabun=X[j][i]/X[i][i]; //後退代入①、②、③ for(k=N-1;k>=0;k--) { X[j][k]-=sabun*X[i][k];//後退代入①、②、③ } } } for(i=0;i<N-1;i++) { X[i][N-1]/=X[i][i]; //後退代入④ X[i][i]/=X[i][i]; } //後退代入ここまで
[実行結果]

以上が今回のガウスの消去法のCコードです。
実のところ、for文の中に5、6行程度計算を入れれば主要な部分は大体完成といえます。
むしろ行の入れ替えの方が計算が複雑になってるような・・
ちなみに、行の入れ替えのところで"解が一意に決まらない"と書いていますが、
例えば3つの変数に対して3つの式を立てても必ずしも解が一意に決まるわけではないため、
その対策として記述しています。
記述がないと式によってはエラーとなる場合もあるので注意しましょう。