大学入試における物理問題の解き方

お初にお目にかかります。2016年4月入社の高橋です。

今回は、私が大学受験をしていた時にやっていた物理の解き方について書いていこうと思います。
このテーマを選んだ理由は後で出てきます。

高校教育課程の物理

普通高校で習う物理は、いろいろな法則や方程式などを学んでいくと思います。

例えば、hの高さにあるボールを自由落下させたときのt秒後の状態について考えます。
そのときボールは上向きを正として
・v=-gt
・x=h-1/2*gt^2
もしくは、速さv0で地上から鉛直投げ上げしたボールのt秒後は
・v=v0-gt
・x=v0t-1/2*gt^2
・v^2-v0^2=2gx
といったような状態が求まります。

高校ですとこれらを「覚えさせられます」。。。

こういうのあまりよろしくないと思うんですよね。
最初物理に触れるときにこういう入り方(微積のカリキュラムも考慮されて)なのは良いと思うのですが、受験物理を解くにあたって方程式を暗記して使うみたいなのだと到底太刀打ちできません。
こういう考え方のままでいると、ちょっと複雑になるとたぶんすぐ思考が止まってしまうんじゃないかと思います。

しかし、過去の偉人たちが観測を元に割り出した基本法則などは覚えなければなりません。
なぜならなにかから計算したわけではないので、様々なアプローチの元になります。四則演算のようなものです。

要するに私が言いたいのは
「覚えることは少なくして楽をしよう」
ということです。

問題へのアプローチ

「図を描け」

短いです。短いですけど大事なことです。
こちらは塾の先生が物理を解くときに大事にしていたことです。

大学入試の問題として出てくる大部分は古典力学です。
図を描いて解けるようになれば力学、電磁気系統の問題はかなり楽に解けるかと思います。
波動系とか量子系に関しては微妙かもしれません。

それでは具体的にどのような図を描けばいいのでしょうか。
下の図を見てください。

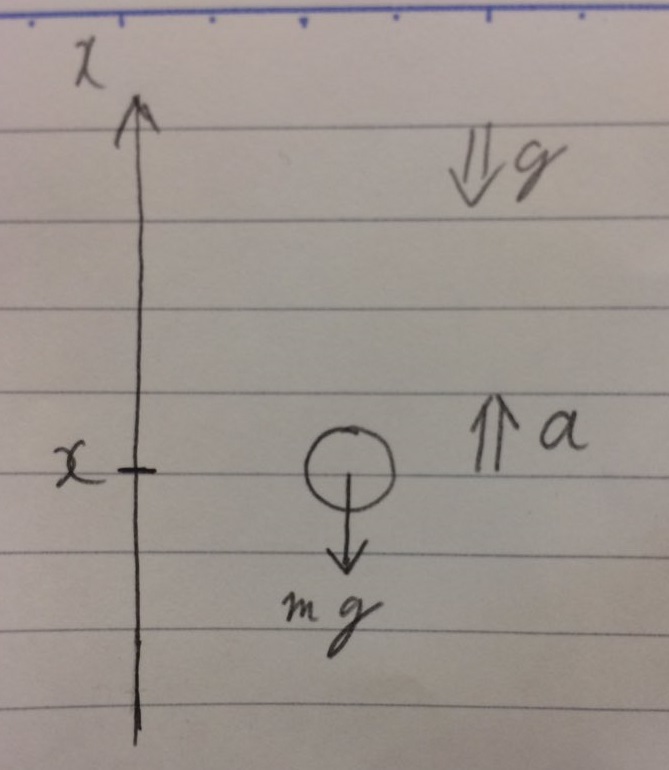
これは重力加速度のある空間で自由運動する物体を考えます。
物体にかかっている外力は重力のみです。

ここで注意する点として、問題を解く人が設定する変数は必ず「軸の正の方向」に対して正と置くようにしましょう。
上向きを正としてる時に下向きの加速度を設定すると、符号の処理が一気にややこしくなります。

図を描いたらやることは簡単で、1方向もしくは直交する2方向に関して運動方程式や力の釣り合いを見ます。
運動方程式とはma=Fです。物理を始めるとき習う最も基本的な方程式です。今回は鉛直方向に当てはめると
・ma=-mg
が方程式となります。

簡単ですね。
このように方程式さえ導出してしまえば、あとは方程式を連立していけば未知数は導き出せます。

両辺をmで割れば加速度aを求めることもできます。
・a=-g
加速度が求まったので積分を行えば
・v=-gt+v0
・x=-1/2*gt^2+v0t+x0
となり速さと変位が求まります。v0,x0は初期値です。
ちなみにこのとき加速度aの設定を軸の向きと逆にすると
d^2x/dt^2=-a
となりすこし面倒です。

次の例を見ていきましょう。

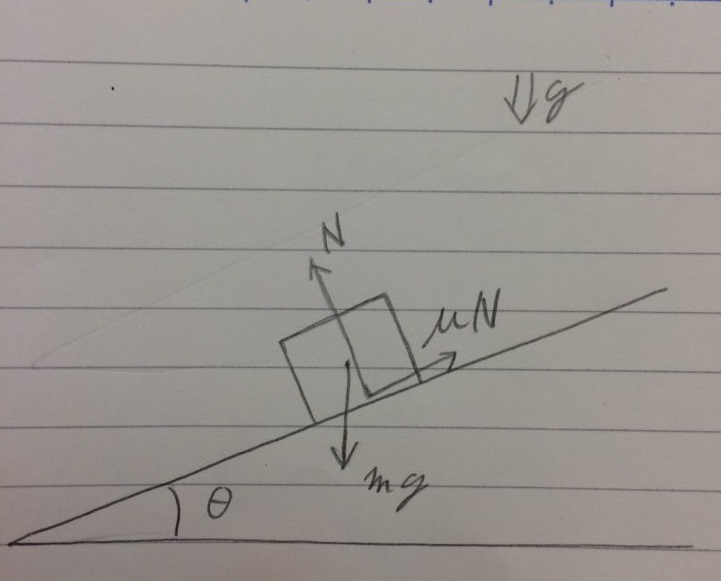
こちらは摩擦の発生する坂の上に物体が静止している状態です。

今回は重力に加え、坂からの垂直抗力と静止摩擦力が加わっています。
先に書いた自由運動とは違い、物体にかかる外力が同軸上にありません。
こういう時は直交2成分に分割して考察します。

どのような2成分を取るかは問題によります。
どのように分けようと答えは導き出せますが、計算の分量は大きく変わります。

今回は坂に対して平行・垂直でとります。こういう問題は坂の上を運動する問題にも発展するので、変数の設定上こちらが楽です。
ただ下の土台が固定じゃない場合は、加速度の設定などで水平・鉛直の方が良かったりしますがそれはまた別の機会にお話しします。

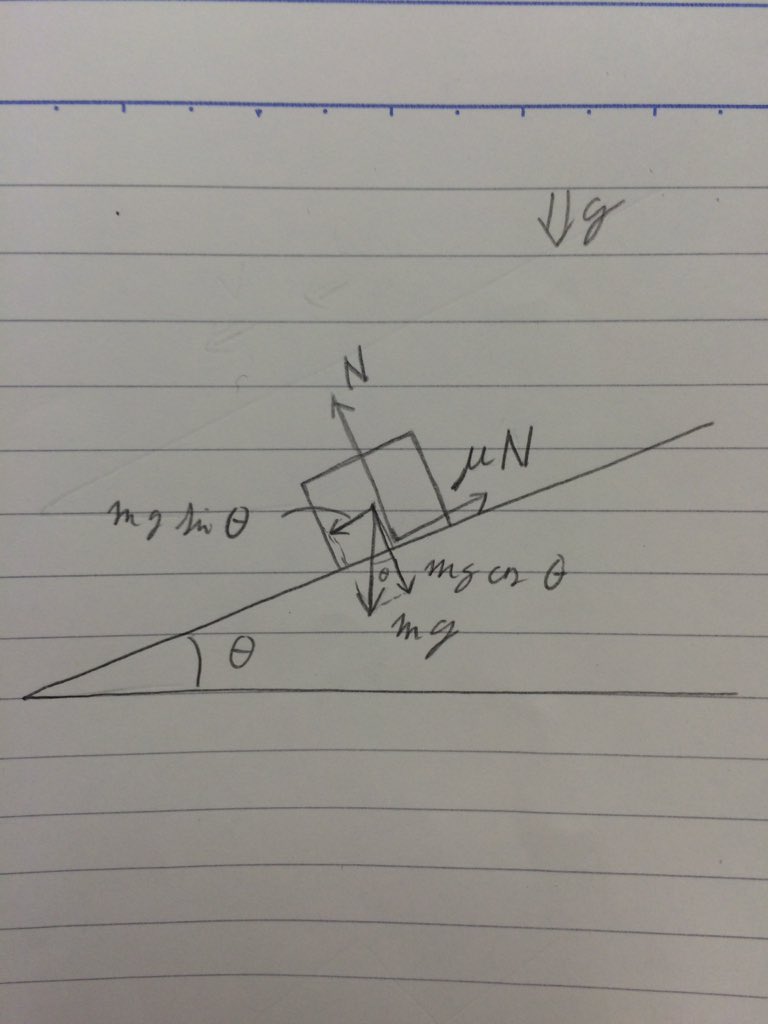
重力を坂の角度θで分解できたので、それぞれの釣り合いの式を見ます。
・mgsinθ=μN
・N=mgcosθ
となります。

最初に「図を描け」と書きましたが、それとセットで図から運動方程式や力のつりあいなどを書き出すことが大切です。
逆に言うとそれをするだけで大概の問題は解けます。

仕事における活躍

さて、わたしがなぜこの題材をブログ記事に選んだかについて触れようかと思います。

今私がかかわっているモデルベース開発というものがあるのですが、ここで使われるModelica言語でこの考え方が有用になってくるのです。

Modelicaはオブジェクト指向言語であり、特徴として非因果的な記述が行えます。
どういうことかというと、(微分)方程式を複数記述すると、それらを連立して求める変数の時間変化が得られるのです。

このように、物理現象を抽象化した図を描き方程式を書き出すということができれば、それをそのままModelicaで記述し計算できるのです。

まとめ

物理現象を解くときには
・図を描く
・方程式を書き出す
の二つを意識しましょう。これだけで大学入試の物理は解けます。
特にめんどくさい誘導にしただけの問題とかはすぐに解けます。

また、物体に働く力をきちんと把握し書き出す技術は、物理現象の理解をより深める助けにもなるので活用しましょう。

次回出番が回ってきたときには、図の描き方を掘り下げるか問題を解いてみるかモデルベース開発に触れていくかを使用と思います。