iPX社員によるブログ

iPX社員が"社の動向"から"自身の知見や趣味"、"セミナーなどのおすすめ情報"に至るまで幅広い話題を投下していくブログ。社の雰囲気を感じ取っていただけたら幸いです。

iPXチャンネル動画解説その１ 「新入社員がやる！Jetson Xavier NX　人物検出ストリーミング」

どうもはじめまして。iPXのYagiです。
iPXチャンネルで投稿している動画について、ブログでも触れていったほうがいいのではないか。という意見が社内で上がり、こうして実際に動画についてのブログ記事を書いていくこととなりました。
まずは、「https://www.youtube.com/watch?v=F2BKpukJO60&t=5s」について触れてみます。

続きを読む

iPXチャンネル動画解説　「CARLAで強化学習シリーズ」

こんにちは、iPXのハナキです。
今回は弊社の公式YouTubeチャンネルの動画「CARLAで強化学習シリーズ」の解説をします。

CARLAで強化学習シリーズとは

この動画シリーズは、CARLA・強化学習の初心者がCARLAのインストールからCARLAを使用した強化学習を実行するまでの様子をまとめたものです。

全3回の動画は下記のような流れになっています。
1.CARLA環境構築編
2.コードの確認と学習の実行
3.学習の精度向上

1.CARLA環境構築編

CARLAで強化学習！ 第一回 CARLA環境構築 - YouTube

第1回はCARLAをインストール・起動確認を行い、強化学習のコードが実行できることを確認するまでとなっています。

インストールや起動確認自体はCARLA公式サイトの手順通りに実行すれば問題なかったのですが、事前準備のUE4とgithubの連携がうまくいかず時間がかかりました。
うまくいかなかった理由は、github連携後のメールがなぜか届かず認証ができなかったためでした…

2. 学習の実行

CARLAで強化学習！ 第二回 コード変更と学習の実行 - YouTube

第2回は強化学習コードを変更しながら学習を実行しました。

観測情報はどうやって取得しているのか、報酬はどうやって計算したらいいのか等の強化学習の基本の部分を理解するために、少しずつコードを変更しながら挙動を確認していました。

第2回動画の観測情報・報酬に使用している値は基本的にはPythonAPIから取得できるものです。

そのため前方目標点・横加速度の追加や報酬関数の割合の変更を行いました。


3.学習の精度向上

CARLAで強化学習！ 第三回 学習の精度向上 - YouTube

第3回は学習の精度向上を行いました。
第2回での挙動を踏まえて、より効率の良い学習を行うために観測情報・報酬関数等の変更をしています。

第3回ではPythonAPIから取得した情報をもとに、学習に有効な数値を出すためにコード内でいくつかの計算を行っています。
ハンドル角速度・横加速度は車両が細かく動いてしまうことを抑制するために追加しました。

また最終走行ではその他変更点として評価周期等を変更しています。
走行開始直後の異常な挙動を抑制するために加速の制限を付け、ステアが振り切れることを抑えるためにアクションの上限下限を変更しました。

振り返って

強化学習をすること自体が初めてだったため、当初はコード内で何を計算しているのか、何の情報があればいいのかということが分からず苦戦しました。
この動画以降業務でも強化学習を行うことが増え、動画撮影時よりも多少は知識が増えました。
この記事を書くために動画を見直してみると、もっとこうしたら良かったんじゃないかなと思うことは多々あります。

おわりに

今回紹介した動画以外にも、iPXの公式チャンネルでは社員が撮影した様々なジャンルの動画があるのでぜひ見てください。
iPXチャンネル - YouTube

iPXチャンネル動画解説その２ 「新入社員がやる！　PERCEPTION NEURON PROで遊んでみた」

iPXのYoshikiです。
iPXのYouTubeチャンネルで投稿している動画の解説記事になります。
この記事では、モーションキャプチャを使用した動画投稿について触れていきます。

モーションキャプチャ

動画の中でも触れているので詳細は省きますが、動画内に登場しているモーションキャプチャは
NOITOM(ノイトム)社製のモーションキャプチャ、
PERCEPTION NEURON PRO(パーセプションニューロンプロ)を使用しています。
こちらは慣性センサ式のものになっており、ジャイロスコープ、加速度計、磁力計を備えたIMU（慣性計測装置）を内蔵しています。専用ソフトのAXIS NEURON PROを使用することで、キャリブレーションやデータの記録、出力を行うことができます。

動画概要

現在公開しているモーションキャプチャに関する投稿は2件あります。
それぞれについて簡単に概要を説明します。
新入社員がやる！ PERCEPTION NEURON PROで遊んでみた - YouTube
こちらはモーションキャプチャを使って撮った初めての動画です。
元々は運転者の姿勢を取得しようと購入したモーションキャプチャですが、車内ではうまく姿勢が得られず倉庫に眠っていました。
モーションキャプチャの説明や装着方法、デモンストレーションなどを紹介しています。


新入社員がやる！ 人間ラジコンを作ろう（前編） - YouTube
こちらはモーションキャプチャを使って、何か他のデバイスを動かしたら面白そうと思って撮影した動画です。
当時は会社にロボットアームがなかったので、試しにラジコンを操作させてみようとトライしました。
目指した形としては、人間の動作をコントローラ代わりにリアルタイムでラジコンを動かすことです。
例えば腕を上げたら発進、水平にしたら停止、下げたらバックなど、腕につけられたセンサーの座標位置の変化などをラジコンの操作に当てるといったことを構想していました。

動画投稿に至るまで

カメラを回したらすぐに撮れる訳ではないという現実を実感しました。
毎日投稿しているYouTuberさんはすごいなぁとしみじみ。
特にセンサーの取り付けや動作確認は時間を使いました。センサーは磁気が強いところの近くだとうまく情報が得られず、撮影場所にも苦労しました。

振り返って

2本目のラジコンを操作する動画は、モーションキャプチャの情報をリアルタイムで通信し、ラジコンを操作することを目指していました。しかし通信がうまくいかなかったり、データとコントローラの紐づけがうまくいかなかったりと、技術的な問題もありました。目指した形で投稿できなかったのは悔やまれました。
あれから半年が経ち、技術的にも少し成長した今なら、あの時目指した形で撮影ができるのではと思っています。(後編に期待)
また、撮影までの筋道を立てて準備をし、撮影・編集、投稿と通常の業務フローと変わりはないと思いました。
撮影の不備で再撮影などはまさに手戻りで、ここも一緒・・・(なくさないとダメですね)

最後に

いろいろな人がいろいろな題材で動画を投稿しているので他の動画もぜひご覧ください。

データ取り実験車両の紹介

久方ぶりの投稿でございます。Suzukiです。
私を含め2~3名でデータ取り実験車両を運用しているチームがあり、そこでは社員（社長）からのオーダー（無茶ぶり）を車ほぼ素人達が頑張る姿を紹介します。
その前に、まずは弊社のデータ取り車両について紹介したいと思います。

データ取り実験車両について

自動運転開発のする上で必要になる実車のデータが欲しい。簡単に手に入らない。
自分たちで用意すればいいんだ！と始まった社内プロジェクトです。

取れるデータは？

現在車両に取り付けられている（予定）のセンサーです。

  • CANデータ
  • カメラ情報(前3, 後ろ2)
  • GPS情報、姿勢情報
  • Lidarデータ
  • IRカメラ(準備中)

下の画像は取得したデータ中の前左右カメラ, ステア角, 車速, GPS, 縦横加速度を可視化しているものです。
YouTube iPXチャンネルでも紹介していますので、是非ご覧ください。

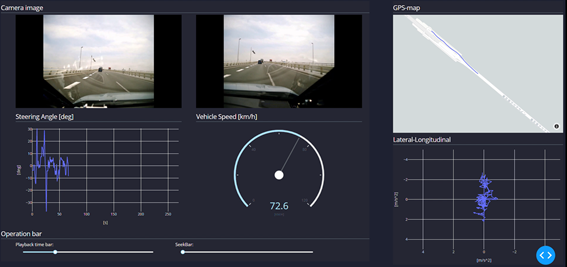
f:id:ipx-writer:20201207182208p:plain
データ取り実験車両

実験車両の表の姿を見せたところで、裏側の本題へGo。

このチームの活動は？

我々の活動は主に「車を走らせてデータを取る」です。

基本的に活動は私とC君の2名です。

  • C君は最近若葉が取れた新人ドライバー
  • 私は免許歴は10年以上あるけど、実質3年ぐらいの一般ドライバー

この2人の運転の「上手さ」や「癖」をデータとして残しています。
また、データを取るときには1つの公道ルートを条件違い(「同じ道を何度も走る」「時間帯・天候が違う」等)で12周以上走るようにしています。

もう一つの活動は、新しいセンサーを付けることです。

時代は日進月歩？であり、注目されるセンサー, お客様が欲しがっていそうなデータをすぐに付けられるのは自社で車両を持っている強みではあります。
取り付けたセンサーは色々ありますが、最近の活動について紹介したいと思います。

センターカメラの取り付け

元々両サイドのフロントカメラしかない車両で、色々データを使っていくうちに「センターカメラの情報欲しいなぁ」と声が上がりました。
会社内にある3DPrinter（社員私物）で治具を作り、簡単じゃーんと甘く見た結果がこちら…

f:id:ipx-writer:20201207184727p:plain
残念なセンターカメラ

図：フロントガラスの反射でダッシュボードがくっきり写っている…

理由は分かるが、どうすりゃいいんだ…
あ、先人の知恵を借りよう（Google画像検索…）
カメラ＋シェードでなんとかなるっぽい！

…出来ました。（3DPrinter万能すぎる）

f:id:ipx-writer:20201207185115p:plain
センターカメラ治具

※切削・研磨中なのでレンズにシールがついています。

画像はないのですが、サイドの淵がカメラの左右下に入り込んでいるのでこれを削ればきっといける。はず…

IRカメラの取り付け

IRカメラはセンサーの特性上ガラス越しには見えません。
なので、車外に取り付けなければならないのですが、非防水品（　＾ω＾）・・・

f:id:ipx-writer:20201207185638p:plain
IRカメラpos

フロントグリルは水がバンバン入ってくるのは分かっていますが、屋根があるだけましかな？
取ってみるとC君がばっちり写るじゃないか。

f:id:ipx-writer:20201207185534p:plain
C君ブログデビュー

写真のｃさんの様に眼鏡を通すと真っ黒になってしまいます。

決まったぜ。と社長に報告したら、
目線の高さがいいな


…え？


ピラーに取り付ける検討を明日から頑張ろうと思い今回の私の記事を終えたいと思います。
コロナ収束したら遠出したいですねぇ～（データ取り）

社内システム管理側から見たテレワーク

こんにちわ、 iPX のコクブンです。
最近は社内のシステム管理を中心に作業を行っています。そこで、今回はシステム管理の立場から「テレワーク」について思うことを書き連ねてみたいと思います。

続きを読む

思考、あるいは学習の"性能"

お久しぶりです。堀田です。
他のブログ記事でもたびたび紹介されていますが、弊社では機械学習を用いた案件や展示をいくつか取り組んできました。

数年前のブレイクスルーで持て囃された時期と比較すると落ち着いてきたような印象は受けますが、各所で研究は続けられており様々な手法が提案されています。
しかし、高精度な手法が出てきても要求されるコンピューターの性能がとんでもないものばかりだったり……
例えば、弊社ではオートモーティブワールドにて自己教師あり学習についての展示を行いましたが、自己教師あり学習の代表的な手法であるSimCLRの論文（https://arxiv.org/pdf/2006.10029.pdf）では128 Cloud TPUという機械学習分野に明るくない人にとってはなんかすごそうとしか分からないようなコンピューターが用いられています。

そこで、今回は機械学習にコンピュータースペックがどれくらい必要なのか、簡単に紹介しようと思います。

続きを読む

Behavior CloningとGAILについて

久しぶりの投票になりますが、パルハットです。今回強化学習関連のテーマでの内容になります。最近複数のプロジェクトが強化学習関連の案件でした。主のstable baselinesという強化学習関連のフレームワークを使っていました。そこで色々DQN(Deep Q Network)とかPPO2(Proximal Policy Optimization)といったアルゴリズムを使ったていましたが、今回のメイン内容はBehavior CloningとGAILGenerative Adversarial Imitation Learningの紹介です。

Behavior CloningとGAIL

Behavior Cloningは行動を真似て学習する方法の一種類であります、摸倣学習とも言われています。摸倣学習といえば逆強化学習もありますが、それ以外にGAILも摸倣学習の一種類です。逆強化の場合エキスパートとの行動履歴から報酬を推定するように学習を行います。一方Behavior CloningとGAILは教師あり学習みたいにエキスパートの行動履歴を正解データとして使って損失関数を最小化しながら、上手に摸倣できたらいい報酬を与えるようになっています。Behavior CloningとGAILの場合エキスパートの行動履歴に主にPIDコントローラもしくは人間による手作業からえられてたデータを使うことになっています。 BCとGAILの実行例は概ね一緒です。

エキスパートのデータを作成

一番最初はエキスパートの履歴データを作成します。状況によってPIDによってデータを作成するか、人間の手作業によってデータを作成するかはわかりますが、私が関わった案件でPIDによってエキスパートのデータを履歴を作成したことがあります。その場合stable-baselinesが提供しているメソッドを使えば簡単にデータを作成できます。

env = gym.make('Pendulum-v0')
def dummy_expert(_obs):
    return env.action_space.sample()

generate_expert_traj(dumpy_expert, 'dummpy_expert_pendulum', env, n_episodes=10)

ここからdummy_expert_pendulum.npzというエキスパート履歴データが作成されます。次のステップでそれを用いて学習を行う。

Behavior Cloningを用いてPre-Train（転移学習）を行う

エキスパートの履歴をデータを読んで、データ・セットを作成する。

dataset = ExpertDataset(expert_path='dummpy_expert_pendulum.npz',
                        traj_limitation=1, batch_size=128)

次に使えたアルゴリズムを用いて学習を回しす。純粋のBehavior cloningの場合PPO2等使って転移学習をおこないます、GAILの場合そのまま使います。

model = PPO2('MlpPolicy', 'Pendulum-v0', verbose=1)
model.pretrain(dataset, n_epochs=1000)
#GAILの場合
model = GAIL('MlpPolicy', 'Pendulum-v0', dataset, verbose=1)
model.learn(total_timesteps=1000)
model.save("gail_pendulum")

実際の実行例

以下のコードをそのまま実行したら確認可能です。

import gym

from stable_baselines import GAIL, SAC
from stable_baselines.gail import ExpertDataset, generate_expert_traj

model = SAC('MlpPolicy', 'Pendulum-v0', verbose=1)
generate_expert_traj(model, 'expert_pendulum', n_timesteps=100, n_episodes=10)

dataset = ExpertDataset(expert_path='expert_pendulum.npz', traj_limitation=10, verbose=1)

model = GAIL('MlpPolicy', 'Pendulum-v0', dataset, verbose=1)
model.learn(total_timesteps=1000)
model.save("gail_pendulum")

del model

model = GAIL.load("gail_pendulum")

env = gym.make('Pendulum-v0')
obs = env.reset()
while True:
  action, _states = model.predict(obs)
  obs, rewards, dones, info = env.step(action)
  env.render()

まとめ

今回強化学習関連内容でした、現在ウチの周り皆強化学習をやっているので、IT業界でも結構熱いテーマになっています、と言っても直接AIに絡んで来るので、これからも強化学習関連の新しい技術が関心を持つでしょう。ということで今回はここまでにさせていただきます。