ガウスの消去法をCで作ろう
今週のブログ担当のシロハと申します。
今回はいたって普通に"C言語”で”ガウスの消去法”のプログラムを作ろうと思います。
ガウスの消去法というと何?と思う方もいるかもしれませんが、
中身は「中学や高校で習う連立方程式を解くこと」と同じです。
ガウスの消去法よりも掃き出し法といったほうがなじみがあるかもしれませんね。
実際に計算してみる
ではプログラムを作る前に、簡単にガウスの消去法の計算プロセスについてのお話をします。
ガウスの消去法は2つのプロセスに分かれており、
1:前進消去
2:後退代入
と呼ばれる計算プロセスとなります。
ただし、先ほども述べたよう中・高で習う程度の計算であり内容はそんなに難しくありません。
ではプログラムを作る前に、まずは以下の例題を実際に計算してみます。
例:3x+6y+2z=32
x+2y+8z=40
7x+3y+3z=35
また後でコード化することも考えて、計算手順も示します。
今回の説明では、それぞれの要素を以下のように記述します

ではまず前進消去から始めます。
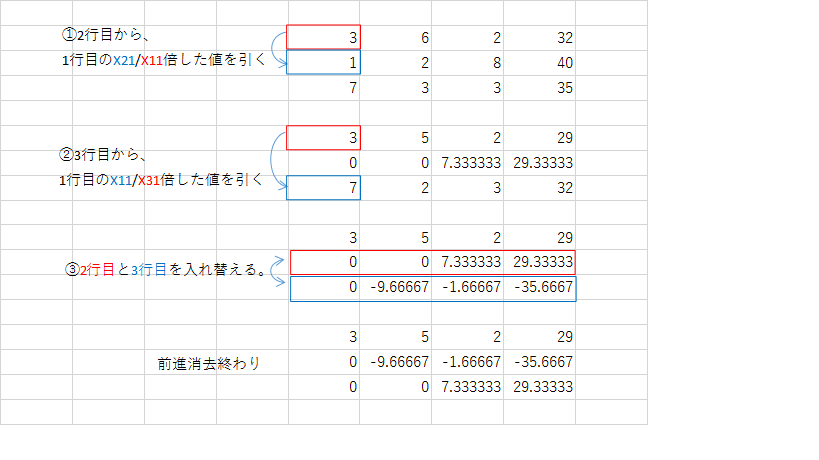
以上が前進消去の計算です。
このように、前進消去では左下部分を全て0にします。
また、前進消去では行の入れ替えが必要な場合もあります。
では次は後退代入です。

これで連立方程式の解を求めることが出来ました。
Cコードを書いてみる
計算の手順は分かったのでCコードを書いてみます。
#include <stdio.h> #include <math.h> #define N 4 void main(void) { int i=1,j=1,k=1,l=0,m=0; int end=0; //解がない時のフラグとして使用 double X[N][N],Y[N][N];//配列(Xは係数、Yは前進消去計算で行を入れ替えるときに使う) double sabun=0; //式の入力 X[0][0]=3;X[0][1]=6;X[0][2]=2;X[0][3]=32; X[1][0]=1;X[1][1]=2;X[1][2]=8;X[1][3]=40; X[2][0]=7;X[2][1]=3;X[2][2]=3;X[2][3]=35; for(i=0;i<N-1;i++) { for(j=0;j<N;j++) Y[i][j]=0; //配列Yの初期化 } //ここまで式入力 //前進消去 for(i=0;i<N-2;i++) { if(X[i][i]==0) //対角要素が0(前進消去③の入れ替えを行う判定) { for(l=i+1;l<N;l++) //入れ替え先を探す { if(X[l][l]!=0) //0ではない場所を見つけた { for(m=0;m<N;m++) //行の入れ替え { Y[i][m]=X[i][m];//入れ替え元を保存 X[i][m]=X[l][m]; X[l][m]=Y[i][m]; } break; } else if(l==N-1) { printf_s("解が一意に決まらない"); end=1; break; } } }//行の入れ替えはここまで for(j=i+1;j<N-1;j++) { sabun=X[j][i]/X[i][i]; //前進消去①、② for(k=i;k<N;k++) { X[j][k]-=sabun*X[i][k];//前進消去①、② } } if(end==1)break; //解が決まらないため計算終了 } //前進消去ここまで //後退代入 for(i=N-2;i>0;i--) { if(end==1)break; //解が決まらないため計算しない for(j=i-1;j>=0;j--) { sabun=X[j][i]/X[i][i]; //後退代入①、②、③ for(k=N-1;k>=0;k--) { X[j][k]-=sabun*X[i][k];//後退代入①、②、③ } } } for(i=0;i<N-1;i++) { X[i][N-1]/=X[i][i]; //後退代入④ X[i][i]/=X[i][i]; } //後退代入ここまで
[実行結果]

以上が今回のガウスの消去法のCコードです。
実のところ、for文の中に5、6行程度計算を入れれば主要な部分は大体完成といえます。
むしろ行の入れ替えの方が計算が複雑になってるような・・
ちなみに、行の入れ替えのところで"解が一意に決まらない"と書いていますが、
例えば3つの変数に対して3つの式を立てても必ずしも解が一意に決まるわけではないため、
その対策として記述しています。
記述がないと式によってはエラーとなる場合もあるので注意しましょう。