Rustでデカルトの葉
近況
また出番が回ってきました砂子です。もう何回目の投稿になるのでしょうか?
今年は本当に暑いですね。普段エアコンは極力使わないようにしてきまたが、 さすがに暑かったのでを久しぶりに電源をいれ涼もうしました。しかし、どう も調子が悪いようなので修理を依頼しました。立ち会いの都合などで、一週間 ほど故障した状態が続いたのですがなんだか無性に暑く感じました。
新言語
さて、私はプログラマーであるわけで当然プログラム言語を記述して仕事をし ております。職務として長らく使ってきたのはC#言語となります。現職務は WEB開発のフロントエンドを担当しているのでTypeScriptをメインとしており ます。思えば、どちらもマイクロソフトに縁が深い言語ですね。
上記2つの言語を深く理解するのも大事ですが、新しいプログラミング言語を 習得し知見を広げることも大事と考え、Rustというものを学習をしてお ります。目下のところ、The Bookと呼ばれるオンラインドキュメントを 読みつつ学習しています。
公式ページにあるように速度、安全性、並行性を目的としてプログミン グ言語であるようです。最も学習を初めて間もないため3つのうち安全性に関 連した要素しか実感できておりません。此の実感した要素は安全性に関連する 「所有権」です。恐らく大半の言語では聞かない概念であると思います。
まあ、実感したというのはコードを書くうえで面倒だったということです。習得 しているプログランミング言語にもよりますが、2つ目以降の言語としてRust を学習する方々は必ずこの所有権の概念で同じことを思うでしょう。
Rustの学習がて簡単なプログラムを書いてこのブログ記事にしよと考えたち、 なにが題材としてよいか自宅にある書籍を物色しました。
デカルトの葉
いくつか書籍を眺めていたら古典的難問に学ぶ微分積分の序章にデカル トの葉が描かれてるのが目に止まりました。曲線を描くというのも難易度とし 難しくないと考えこれを題材にしようと考えました。
デカルトの葉とはWikipediaではデカルトの正葉線として説明がなされて いる代数曲線になります。大学で微積分を学んだ方なら教科書に描かれていたもの が記憶に残っているのではないでしょうか?
直行座標の方程式による定義は下記のようになります。
上記の数式はまたパラメータ表示として下記のようにも表わされます。
また、第一象限のループで囲まれる面積は下記のようになります。
そこで3つのことをRustで実現しよう。
- パラメータ表示による曲線のプロット
- 直行座標の方程式を使用した乱数による曲線のプロット
- ループで囲まれる面積の乱数を使用した近似値の計算
なお、以降ではとして計算する。
Rust 準備
Rustのインストール等の説明は公式ページを見てください。 以下ではプロジェクト作成と使用したライブラリだけを記述します。
プロジェクトを作成。引数でライブラリではなく実行可能なアプリとして設定しています。
cargo new folium_of_descartes --bin
使用する外部ライブラリを設定します。 出来上がったプロジェクトフォルダ内のCargo.tomlを下記のように編集します。
[package] name = "folium_of_descartes" version = "0.1.0" [dependencies] gnuplot = "0.0.26" rand = "0.5"
main.rsを編集後、プログラムを実行するには下記コマンド実行です。 初回はCargo.tomlで設定したライブラリのダウンロード等が行われます。 記述ミスがあった場合はこの段階でエラーなり、警告がでます。
cargo run
Rust ソースコード(main.rs)
そして、記述したコードを貼っておく。プロジェクトフォルダに出来上がったmain.rsに記述した。
extern crate gnuplot; extern crate rand; // プロット用のライブラリ use gnuplot::*; // 乱数発生用のライブラリ use rand::prelude::*; use rand::prng::XorShiftRng; //// パラメータにより曲線を描画する fn draw_curve_parameter() { // 3つの範囲で(x,y)を算出 // -100 < t < -2 let ts1 = get_parameter(-100., -2., 0.1); let xs1 = get_x_from_parameter(&ts1); let ys1 = get_y_from_parameter(&ts1); // -0.5 < t < 0.0 let ts2 = get_parameter(-0.5, 0.0, 0.05); let xs2 = get_x_from_parameter(&ts2); let ys2 = get_y_from_parameter(&ts2); // 0.0 < t < 5.0 let ts3 = get_parameter(0.0, 5.0, 0.1); let xs3 = get_x_from_parameter(&ts3); let ys3 = get_y_from_parameter(&ts3); // -5.0 < x < 5.0, -5.0 < y < 5.0 をプロット let mut fg = Figure::new(); // fg.axes2d() .set_aspect_ratio(Fix(-1.0)) .set_x_axis(true, &[]) .set_y_axis(true, &[]) .set_x_range(Fix(-5.), Fix(5.0)) .set_y_range(Fix(-5.), Fix(5.0)) .points(xs1, ys1, &[Color("green")]) .points(xs2, ys2, &[Color("blue")]) .points(xs3, ys3, &[Color("red")]); fg.show(); } /// 指定された範囲のパラメータを取得する fn get_parameter(start: f64, end: f64, step: f64) -> Vec<f64> { let mut tmp = Vec::new(); let mut x = start; while x < end { tmp.push(x); x = x + step; } tmp } /// パラメータに対応したXを取得する fn get_x_from_parameter(ts: &Vec<f64>) -> Vec<f64> { ts.into_iter().map(|t| (3.0*3.0*t)/(1.0+t.powi(3))).collect() } /// パラメータに対応したYを取得する fn get_y_from_parameter(ts: &Vec<f64>) -> Vec<f64> { ts.into_iter().map(|t| (3.0*3.0*t.powi(2))/(1.0+t.powi(3))).collect() } /// 乱数により曲線を描く fn draw_curve_random() { let seed = [0u8; 16]; let mut rng = XorShiftRng::from_seed(seed); let mut xs: Vec<f64> = Vec::new(); let mut ys: Vec<f64> = Vec::new(); let mut i = 10000000; while i != 0 { let x = rng.gen_range(-5., 5.) as f64; let y = rng.gen_range(-5., 5.) as f64; let z = x.powi(3) + y.powi(3) - 3.0 * 3.0 * x * y; if z.abs() < 0.001 { xs.push(x); ys.push(y); } i = i - 1; } let mut fg = Figure::new(); fg.axes2d() .set_aspect_ratio(Fix(-1.0)) .set_x_axis(true, &[]) .set_y_axis(true, &[]) .set_x_range(Fix(-5.), Fix(5.0)) .set_y_range(Fix(-5.), Fix(5.0)) .points(xs, ys, &[Color("blue")]); fg.show(); } /// 第一象限の面積を描く fn draw_area() { // 乱数初期化 let seed = [0u8; 16]; let mut rng = XorShiftRng::from_seed(seed); let mut xs: Vec<f64> = Vec::new(); let mut ys: Vec<f64> = Vec::new(); let size = 100000; let mut i = size; while i != 0 { let x = rng.gen_range(0., 5.) as f64; let y = rng.gen_range(0., 5.) as f64; let z = x.powi(3) + y.powi(3) - 3.0 * 3.0 * x * y; if z < 0.001 { xs.push(x); ys.push(y); } i = i - 1; } // 曲線内部と判定された割合から面積を算出する let area = 5.0 * 5.0 * xs.len() as f64 / size as f64; let mut fg = Figure::new(); fg.axes2d() .set_title(&format!("面積:{}", area), &[]) .set_aspect_ratio(Fix(-1.0)) .set_x_axis(true, &[]) .set_y_axis(true, &[]) .set_x_range(Fix(0.), Fix(5.0)) .set_y_range(Fix(0.), Fix(5.0)) .points(&xs, ys, &[Color("blue")]); fg.show(); } fn main() { draw_curve_parameter(); draw_curve_random(); draw_area(); }
結果
新言語とはいえ単純な文法だけでも曲線は十分に描け、簡単な数値実験を行な うことができた。やはりドキュメントを読むだけでは飽きが来ることや理解の 度合いが感じづらいので簡単なゴールを設定してみるとモチベーションに繋が りやすい。
パラメータ表示による曲線のプロット
パラメータによる曲線の描画は関数draw_curve_parameter()で行った。プロットは下図のようになった。
緑は で第一象限、 青は
で第二象限、赤は
で第4象限となります。

しかし、曲線上に均等に点が描画されると予想したがそうはならなかった。方程式の形で見ているとまるで 曲線上に点が密に分布するイメージを持つがそんなことはなかった。
直行座標の方程式を使用した乱数による曲線のプロット
関数draw_curve_with_random()で乱数で大量の座標を生成し、
に適合する座標のみをプロットした。
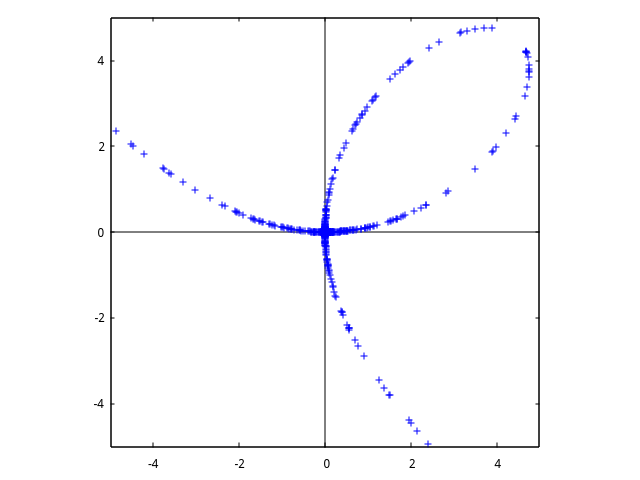
こちらは均等に点が分布にすると考えたがならなかった。考えてみれば曲線の変化率は場所ことに違うので確かに均等に分布しないことになる。つまり、ある曲線の部分では変化率が小さいため上記の判定が真になる面積が大きいが、またある場所では変化率が大きいため上記判定で真になる面積は少ない。それが場所ごとの点の分布に現れるのではないか?
ループで囲まれる面積の乱数を使用した近似値の計算
関数draw_area_with_random()で第一象限のループ状の内部の面積を求めてみた。
上記曲線描画と同様に乱数で大量の座標を生成し、
で判定された座標の個数と
生成した座標の割合を乱数生成の範囲の面積にかけて算出している。
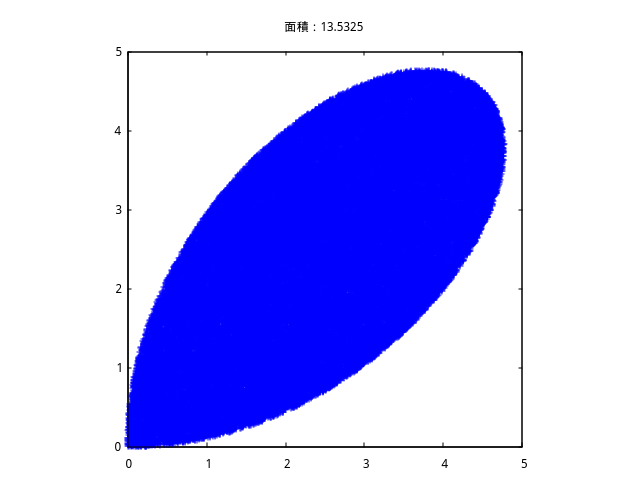
期待値はであるので、近似値がえられている。
所感
学習中のプログラミング言語でも自分としては有益な結果がでた。学生時代にこうゆうことをやっていれば微積分にも もっと興味をもって取り組めたのではないだろうか?
Rustの習熟度は正直かなり問題ありですね。いろいろあるが早急に下記は対応したい。
- ドキュメント、コメントの書き方
- ライブラリのドキュメントの読み方
- 開発環境(Emacs)の整備
曲線の描画は興味深いテーマであったと思う。Rustの学習を進めながら曲線を調べて描画を行っていこう。 できれば学生時代の卒論であつかったMD6の実装を最終ゴールとしたい。ではこれにて。